ट्रेडिंग रणनीतियों में फिबोनाकी स्तर और उनका अनुप्रयोग

फिबोनाकी स्तर वित्तीय बाजारों के तकनीकी विश्लेषण का एक एकीकृत भाग बन गए हैं।ट्रेडर्स उनका उपयोग संभावित समर्थन और प्रतिरोध स्तरों, मूल्य पाइवट पॉइंट्स, रुझान अवधियों, और लाभ अर्जित करने के लिए इष्टतम क्षणों की पहचान करने मेंएक टूल के रूप में करते हैं।मेटाट्रेडर4 (MT4) प्लेटफॉर्म में, अंतर्निहित ग्राफिक टूल्स के बीच, आप फिबोनाकी रिट्रेसमेंट आरेखित करें विकल्प प्राप्त कर सकते हैं।यह टूल ट्रेड किए गए असेट्स की गति का पूर्वानुमान लगाने में सहायता करता है, इस परिकल्पना के आधार पर कि बाजार चक्रों में गति करता है और मूल्य सुधार लियोनार्डो फिबोनाकी द्वारा खोजे गए प्रतिमान का सामान्यत: पालन करता है।

एक संक्षिप्त इतिहास

फिबोनाकी अनुक्रम के इतिहास, इसके अद्भुत गुण, और "दैवीय" स्वर्ण अनुपात से इसके संबंध का वर्णन एक पृथक आलेख में किया गया। हमने उल्लेख किया कि इस अनुक्रम का परिचय इतालवी गणितज्ञ पीसा के लियोनार्डो, जिन्हें फिबोनाकी के रूप में भी जाना जाता है, द्वारा 13वीं सदी में यूरोपीय विज्ञान में दिया गया। यह 0 और 1 से प्रारंभ होता है और प्रत्येक अनुवर्ती संख्या दो पूर्ववर्तियों (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, इत्यादि) का योग होती है। उसी आलेख में, हमने हमारे जीवन के विभिन्न क्षेत्रों: गणित, भौतिकी, रसायन, साइबरनेटिक्स, वास्तु, जीवविज्ञान, और संगीत में भी इस संख्यात्मक श्रृंखला के अनुप्रयोग की चर्चा की। अब, हम फॉरेक्स, स्टॉक, क्रिप्टोकरेंसी और कॉमोडिटी बाजारों के साथ फिबोनाकी संख्याओं के संबंध की चर्चा करेंगे।

वित्तीय बाजारों में फिबोनाकी अनुक्रम का उपयोग स्वयं गणितज्ञ का मूल विचार नहीं था। इन सिद्धांतों के अनुप्रयोग की संभावना सबसे पहले स्टॉक बाजार और फिर अन्य वित्तीय बाजारों में खोजी गई और लोकप्रियता 20वीं सदी में ही मिली। इस अनुक्रम का उपयोग करना प्रारंभ करने वाले प्रथम व्यक्तियों में से एक राल्फ एलियट, एलियट तरंग सिद्धांत के विकासकर्ता थे। हालाँकि, फिबोनाकी स्तर अन्य विश्लेषकों के कार्यों के कारण सर्वाधिक विस्तीर्ण बन गए, जिनके नाम का उल्लेख हम आलेख के अंत में करेंगे।

फिबोनाकी रिट्रेसमेंट स्तर

इतालवी गणितज्ञ के नाम पर तकनीकी विश्लेषण में सर्वाधिक लोकप्रिय टूल फिबोनाकी रिट्रेसमेंट स्तर है, जिनका उपयोग मुख्य रुझान से मूल्य सुधार की सीमा का निर्धारण करने के लिए किया जाता है। सर्वाधिक आम रिट्रेसमेंट स्तर 23.6%, 38.2%, 50%, 61.8%, और कभी-कभी 78.6% हैं। इन स्तरों को लागू करने के लिए, सबसे पहले व्यक्ति को मूल्य चार्ट पर मुख्य रुझान की पहचान करना चाहिए। फिर, MT4 टर्मिनल में, फिबोनाकी रिट्रेसमेंट आरेखित करें टूल इस रुझान के दो चरम बिंदुओं: एक ऊपरी रुझान के लिए न्यूनतम और अधिकतम अथवा एक निचले रुझान के लिए अधिकतम और न्यूनतम पर लागू किया जाता है। चार्ट पर परिणामी फिबोनाकी स्तर संभावित क्षेत्रों की पहचान करने में सहायता करते हैं जहाँ मूल्य समर्थन अथवा प्रतिरोध का और, तद्नुसार, पलटाव का अनुभव कर सकता है।

एक समझदार पाठक फिबोनाकी संख्याओं और फिबोनाकी रिट्रेसमेंट स्तरों के बीच अंतर पर तुरंत ध्यान देगा। पहली ही झलक में, वे असंबंधित लगते हैं, किंतु यह मामला नहीं है।

– 23.6% स्तर एक गहरे अनुपात के रूप में व्युत्पन्न होता है जब एक संख्या को अनुक्रम में दाईं ओर दो स्थान स्थित संख्या द्वारा विभाजित किया जाता है।

– 38.2% स्तर फिबोनाकी अनुक्रम में किसी संख्या को इसके ठीक दाईं ओर स्थित संख्या द्वारा विभाजित करने से परिणाम देता है। उदाहरण के लिए, 34 को 89 से विभाजित करना लगभग 0.382 देता है।

– 61.8% स्तर (अथवा 38.2% का प्रतिलोम) फिबोनाकी अनुक्रम में एक संख्या को इसके ठीक बाद आने वाली संख्या द्वारा विभाजित करके प्राप्त होता है। उदाहरण के लिए, 89 द्वारा 55 को विभाजित करने पर लगभग 0.618 होता है।

– 50% स्तर फिबोनाकी अनुक्रम लागू करने का एक प्रत्यक्ष परिणाम नहीं है, बल्कि इसकी सरलता और मनोवैज्ञानिक महत्व के कारण इसका उपयोग तकनीकी विश्लेषण में किया जाता है। यह अवलोकन किया गया है कि कीमतें पिछली गति के लगभग आधे द्वारा सुधरती हैं।

– 78.6% स्तर 61.8% का वर्गमूल है।

फिबोनाकी एक्सटेंशन स्तर

फिबोनाकी एक्सटेंशन स्तरों का उपयोग उन संभावित स्तरों का उपयोग करने के लिए किया जाता है जिन तक मूल्य गति एक सुधार के बाद प्राथमिक रुझान की दिशा में जारी रह सकती है। ये स्तर, 161.8%, 261.8%, और 423.6% सहित, इस परिकल्पना पर भी आधारित होते हैं कि बाजार गतियाँ सामान्यत: प्रकृति और गणित में पाए गए अनुपातों का पालन करती हैं। एक्सटेंशंस एक सुधार पूर्ण होने के बाद ट्रेडर्स की पॉजीशनों को बंद करने के लिए लक्ष्यों को पहचानने अथवा लाभ लेने में सहायता करते हैं। यद्यपि फिबोनाकी अनुक्रम से संख्याएँ नहीं, ये स्तर गणितीय गुणों, विशेषकर स्वर्ण अनुपात (1.618), के माध्यम से इससे करीब से संबंधित होते हैं।

– 161.8% स्वर्ण अनुपात को 100 से गुणा करने पर सीधे ही परिणाम देता है। यह एक्सटेंशन स्तर विशेष रूप से महत्वपूर्ण है क्योंकि यह उस स्थान के संगत होता है जहाँ अगली मूल्य गति, स्वर्ण अनुपात सहगुणांक द्वारा गुणित, पिछले रुझान के समानुपातिक हो सकती है। फिबोनाकी अनुक्रम के संदर्भ में, यदि आप कोई संख्या लेंगे और इसे 1.618 से गुणा करेंगे, तो आप अनुक्रम में अगली संख्या के मान का अनुमान लगा लेंगे।

– 261.8% और 423.6% स्वर्ण अनुपात से संबंधित प्रतिशत‍ भी हैं किंतु एक सुधार के बाद लंबे अथवा अधिक चरम लक्ष्य स्तरों को निरूपित करते हैं। उदाहरण के लिए, 261.8% को स्वर्ण अनुपात (1.618) को स्वयं से गुणा करके और फिर 100 से गुणा करके इसे एक प्रतिशत में बदलने के लिए व्युत्पन्न किया जा सकता है। यह स्तर मूल्य गति के लिए एक आगे लक्ष्य इंगित करता है, जो मजबूत रुझानों में विशेष रूप से प्रासंगिक हो सकता है। 423.6% को स्वर्ण अनुपात के आगे गुणन द्वारा अथवा फिबोनाकी संख्याओं के अन्य संयोजनों को स्वयं से और 100 से गुणा करके प्राप्त किया जाता है। यह स्तर और भी चरम लक्ष्य को निरूपित करता है, जिस पर बहुत मजबूत रुझान गतियों की दुर्लभ स्थितियों में पहुँचा जा सकता है।

प्रायोगिक अनुप्रयोग युक्तियाँ

फिबोनाकी रिट्रेसमेंट और एक्सटेंशन स्तर मौसमी ट्रेडर के लिए एक शक्तिशाली टूल हैं जो बाजार व्यवहार की भविष्यवाणी करने की एक उच्चतर संभावना प्रदान करते हैं। हालाँकि, यह याद रखना महत्वपूर्ण है कि, किसी टूल के समान, वे 100% गारंटियाँ प्रदान नहीं करते हैं। इसलिए, कठोर जोखिम प्रबंधन अनुशासन का पालन किया जाना चाहिए, और ट्रेड्स में प्रवेश करने और बाहर निकलने के लिए अधिक विश्वसनीय संकेतों को प्राप्त करने हेतु अन्य तकनीकी विश्लेषण विधियों और संकेतकों जैसे चलायमान औसत (MA), सापेक्ष मजबूत सूचकांक (RSI), MACD, और वॉल्यूम स्तरों के साथ उनका उपयोग किया जाना चाहिए। विभिन्न समय सीमाओं पर विचार करना भी महत्वपूर्ण है। उदाहरण के लिए, दैनिक अथवा साप्ताहिक चार्ट्स पर पहचाने गए फिबोनाकी स्तर अल्पकालिक समय सीमाओं पर पहचाने गए फिबोनाकी स्तरों की तुलना में अधिक महत्वपूर्ण हो सकते हैं, जो अधिक मजबूत समर्थन अथवा प्रतिरोध स्तर प्रदान करते हैं।

किसी फिबोनाकी स्तर के आधार पर किसी ट्रेड में प्रवेश करने का निर्णय करने के पूर्व, संकेतकों, जैसे कैंडलस्टिक्स प्रतिमानों, की पुष्टि होने की प्रतीक्षा करना उचित है। इसके अतिरिक्त, फिबोनाकी रिट्रेसमेंट आरेखित करें टूल लागू करते समय, प्रारंभिक और समाप्ति बिंदु का सुधार चयन महत्वपूर्ण है। महत्वपूर्ण ऊँचाइयों और निम्नताओं को, जो चार्ट पर स्पष्ट रूप से परिभाषित शीर्ष अथवा गर्त हैं, चुना जाना चाहिए।

यह समझना आवश्यक है कि जहाँ फिबोनाकी स्तर उपयोगी बेंचमार्कों को प्रदान कर सकते हैं, वहीं बाजार उनका हमेशा अनुमानत: प्रतिसाद नहीं देता है, क्योंकि वे एक कठोर कानून की बजाय एक मनोवैज्ञानिक घटक को निरूपित करते हैं। इसलिए, ट्रेडर्स को अनपेक्षित गतियों के लिए तैयार रहना चाहिए और तद्नुसार जोखिम प्रबंधित करना चाहिए। स्टॉप लॉस और टेक प्रॉफिट ऑर्डर्स स्थापित करके उनकी सहायता की जा सकती है। उदाहरण के लिए, एक स्टॉप लॉस को झूठे ब्रेकआउट्स के विरुद्ध रक्षा करने के लिए एक मुख्य फिबोनाकी स्तर से ठीक परे रखा जा सकता है।

तकनीकी विश्लेषण टूल्स

फिबोनाकी स्तरों पर आधारित कई टूल्स हैं। फिबोनाकी रिट्रेसमेंट ट्रेडर्स के बीच संभवत: सर्वाधिक लोकप्रिय है, जिसकी हमने पहले ही चर्चा की है। इसे मेटाट्रेडर 4टर्मिनल में एकीकृत किया जाता है, जहाँ इसे फिबोनाकी रिट्रेसमेंट आरेखित करें कहा जाता है। अन्य टूल, फिबोनाकी एक्सटेंशन, की भी चर्चा की गई है।

फिबोनाकी प्रोजेक्शंस फिबोनाकी एक्सटेंशन के समान टूल है। अंतर यह है कि यह गति की पिछली तरंगों के आकार और दिशा के आधार पर बाद वाली मूल्य गति का आकलन लगाने का एक तरीका प्रदान करता है। भावी गति की भविष्यवाणी करने के लिए, एक व्यक्ति को पिछली तरंग में तीन बिंदुओं का चयन करना चाहिए: गति की शुरुआत, गति का अंत, और सुधार का अंत बिंदु।

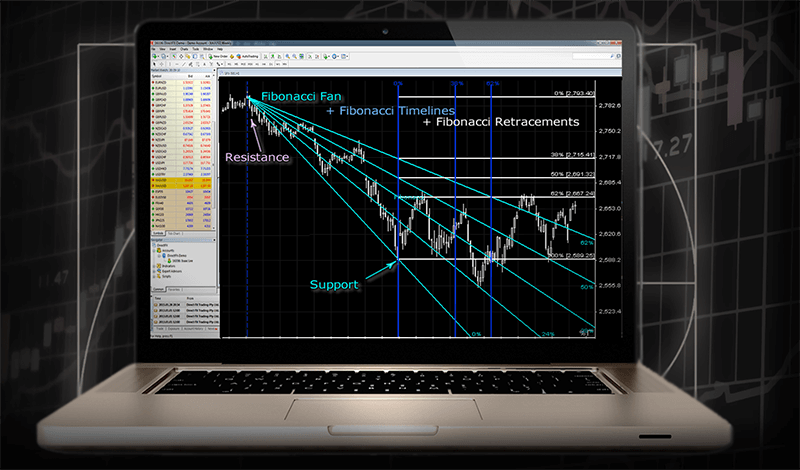
अन्य, फिबोनाकी फैन, में चार्ट पर फिबोनाकी रिट्रेसमेंट स्तरों के माध्यम से एक बिंदु (आमतौर पर एक महत्वपूर्ण न्यूनतम अथवा अधिकतम) से खींची गई रेखाएँ होती हैं। फैन रेखाएँ संभावित समर्थन अथवा प्रतिरोध रेखाओं के रूप में कार्य कर सकती हैं।

अंत में, फिबोनाकी टाइम जोन, तकनीकी विश्लेषण के लिए एक काफी असामान्य टूल, का उपयोग गुजरे हुए समय के आधार पर संभावित उलट क्षणों की पहचान करने के लिए किया जाता है। जोनों में विशिष्ट समय अंतरालों पर स्थित उर्ध्वाधर रेखाओं की एक श्रृंखला होती है, जो फिबोनाकी अनुक्रम के संगत होती हैं और सुझाव देती हैं कि महत्वपूर्ण उलट बिंदु इन क्षणों पर घटित हो सकते हैं।

जैसा कि पूर्व में कहा गया है, ये टूल्स, अन्य के समान, भावी मूल्य गतियों की एक सटीक भविष्यवाणी की गारंटी नहीं देते हैं। वे केवल ट्रेडिंग परिचालनों की योजना बनाते और ट्रेडिंग रणनीतियाँ विकसित करते समय विचार करने के लिए संभावित स्तर प्रदान करते हैं। सूचीबद्ध टूल्स के सफल अनुप्रयोग के लिए अभ्यास, धैर्य, अनुशासन और बाजार परिस्थितियों की एक गहरी समझ की आवश्यकता होती है।

थोड़ी और इतिहास: 13वीं से 20वीं सदी तक

मुख्य गणितीय शोध प्रबंध, "लाइबर अबाकी" (गणना की पुस्तक), 1202 में फिबोनाकी द्वारा लिखी गई, जिसका संशोधित संस्करण 1228 में आया। यह पुस्तक दशमलव अंकगणित की व्याख्या और प्रचार को समर्पित थी और इसने शून्य संख्या के निरूपण सहित भारतीय-अरबी संख्याओं के विस्तार के लिए नींव डाली। इस कार्य में, खरगोश जनसंख्या वृद्धि के बारे में समस्या का समाधान करते समय, फिबोनाकी ने प्रसिद्ध अनुक्रम का निर्माण किया जिसमें उनका नाम आता है और गणित के लिए उनका सर्वाधिक महत्वपूर्ण योगदान बन गया है।

फिबोनाकी अनुक्रम ने 20वीं सदी में वित्तीय बाजारों की ट्रेडिंग में नए अनुप्रयोग पाए, प्राथमिक रूप से कई ट्रेडर्स और वित्तीय विश्लेषकों के कारण जिन्होंने इसका अध्ययन किया और इसका अपने कार्य में उपयोग किया। उनमें से अधिकांश मूल्य प्रतिमानों वाले फिबोनाकी स्तरों और एलियट तरंग सिद्धांत से संबद्ध थे। यद्यपि राल्फ एलियट का कार्य पुनरावर्ती प्रतिमानों और अनुक्रमों पर आधारित है, तथापि यह चर्चा किए गए अनुक्रम से एक संबंध रखता है। एलियट ने खोजा कि बाजार तरंग प्रतिमान फिबोनाकी संख्याओं से कुछ-कुछ संबंधित एक संरचना का पालन करते हैं। उदाहरण के लिए, तरंगों को 5 और 3 के अंशों में विभाजित करना, जिनका योग 8 तक आता है, फिबोनाकी अनुक्रम का भाग है। एलियट के अनुयायी, रॉबर्ट प्रेचर, ने यह दावा करते हुए कि बाजार तरंगें भीड़ मनोविज्ञान का पालन करती हैं, स्पष्ट रूप से प्रदर्शित किया कि वास्तव में इन प्रतिमानों की भविष्यवाणी फिबोनाकी संख्याओं का उपयोग करते हुए की जा सकती है।

लैरी पेसैवेंटो ने तकनीकी विश्लेषण में फिबोनाकी स्तरों के उपयोग को लोकप्रिय बनाने के लिए एक महत्वपूर्ण योगदान दिया। इस ट्रेडिंग अनुभवी ने गुणावृत्ति मूल्य प्रतिमानों की खोज करते हुए कई पुस्तकें लिखीं, जिनमें से कई इतालवी गणितज्ञ के अनुक्रम से निकटता से जुड़ी हैं। स्कॉट कार्ने ने भी फिबोनाकी स्तरों के आधार पर कई गुणावृत्ति प्रतिमानों का विकास किया, जैसे "बटरफ्लाय" और "क्रैब"। फिलिप कारेट के योगदान को भी नहीं भूलना चाहिए। पायोनियर फंड के संस्थापक ने बाजारों का विश्लेषण करने के लिए गणितीय सिद्धांतों का उपयोग किया, और दीर्घकालिक विश्लेषण और स्टॉक चयन पर आधारित, निवेश करने की उनके तरीके ने, "स्वर्ण अनुपात" की खोज के समान सिद्धांतों को परिलक्षित किया।

***

अंत में, आइए कुछ कथन प्रस्तुत करें जो वित्तीय विश्लेषण में फिबोनाकी स्तरों के महत्व और उपयोगिता पर कई ट्रेडर्स और विश्लेषकों की आम राय को परिलक्षित करते हैं:

– "फिबोनाकी अनुक्रम ब्रह्मांड का प्राकृतिक क्रम है, और इसप्रकार भावी गतियों की भविष्यवाणी करने के लिए वित्तीय बाजारों पर इसे लागू करना उचित है।"

– "फिबोनाकी रिट्रेसमेंट स्तर ट्रेडिंग की पवित्र कब्र नहीं हैं, बल्कि वे बाजार मनोविज्ञान और संभावित पलटावों को समझने के लिए अद्वितीय रूप से उपयोगी हैं।"

– "फिबोनाकी एक्सेंटशंस एक ट्रेडिंग बाजार में लाभ लक्ष्यों को स्थापित करने के लिए अमूल्य हैं जो वह दिशा प्रदान करते है जहाँ तक मूल्य आगे जा सकते हैं।"