Fibonacci මට්ටම් මූල්ය වෙලඳපොලවල තාක්ෂණික විශ්ලේෂණයේ අනිවාර්ය අංගයක් බවට පත්ව ඇත. වෙළඳුන් ඒවා සිදුවිය හැකි ආධාරක සහ ප්රතිරෝධ මට්ටම්, මිල හැරවුම් ලක්ෂ්ය, ප්රවණතා කාලසීමාවන් සහ ලාභ ලබා ගැනීම සඳහා ප්රශස්ත අවස්ථා හඳුනා ගැනීමට මෙවලමක් ලෙස භාවිතා කරයි. MetaTrader 4 (MT4) වේදිකාවේ, ගොඩනඟන ලද ග්රැෆික් මෙවලම් අතර, ඔබට Draw Fibonacci retracement විකල්පය සොයාගත හැකිය. වෙළඳපල චක්රවල චලනය වන බවට සහ මිල නිවැරදි කිරීම් බොහෝ විට ලියනාඩෝ ෆිබොනාච්චි විසින් සොයා ගන්නා ලද රටාව අනුගමනය කරයි යන උපකල්පනය මත පදනම්ව, වෙළඳාම් කරන ලද වත්කම්වල චලනය පිලිබඳ අනාවැකි පල කිරීමට මෙම මෙවලම උපකාරී වේ.
කෙටි ඉතිහාසයක්
Fibonacci අනුපිළිවෙලෙහි ඉතිහාසය, එහි කැපී පෙනෙන ගුණාංග සහ "දිව්ය" ස්වර්ණමය අනුපාතයට ඇති සම්බන්ධය වෙනම ලිපියකින් විස්තර කරන ලදී. මෙම අනුපිළිවෙල යුරෝපීය විද්යාවට හඳුන්වා දුන්නේ 13 වැනි සියවසේදී ඉතාලි ජාතික ගණිතඥයෙකු වූ පීසාහි ලියනාඩෝ හෙවත් ෆිබොනාච්චි විසින් බව අපි සඳහන් කළෙමු. එය 0 සහ 1 න් ආරම්භ වන අතර, සෑම පසු අංකයක්ම පෙර ඇති ඒවා දෙකේ එකතුව (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, සහ තවත්) වේ. එම ලිපියේම, මෙම සංඛ්යාත්මක ශ්රේණිය අපගේ ජීවිතයේ විවිධ ක්ෂේත්රවල යෙදීම පිළිබඳව අපි සාකච්ඡා කළෙමු: ගණිතය, භෞතික විද්යාව, රසායන විද්යාව, සයිබර්නෙටික්, ගෘහ නිර්මාණ ශිල්පය, ජීව විද්යාව සහ සංගීතය පවා. දැන්, අපි ෆොරෙක්ස්, කොටස්, ක්රිප්ටෝ මුදල්, සහ commodity Markets සමඟ Fibonacci අංක සම්බන්ධ කිරීම පිළිබඳව සාකච්ඡා කරමු.
මූල්ය වෙලඳපොලවල Fibonacci අනුපිළිවෙල භාවිතා කිරීම ගණිතඥයාගේම මුල් අදහස නොවේ. මෙම මූලධර්ම මුලින්ම කොටස් වෙළඳපොලට සහ පසුව අනෙකුත් මුල්ය වෙලඳපොලවල් වලට යෙදීම ගවේෂණය කර ජනප්රියත්වයට පත් වූයේ 20 වන සියවසේදී පමණි. මෙම අනුපිළිවෙල භාවිතා කිරීම ආරම්භ කළ පළමු අයගෙන් කෙනෙකු වූයේ Elliott Wave න්යායේ සංවර්ධකයා වන Ralph Elliott ය. කෙසේ වෙතත්, Fibonacci මට්ටම් වඩාත් පුලුල්ව පැතිර ගියේ අනෙකුත් විශ්ලේෂකයින්ගේ කෘතීන්ට ස්තූතිවන්ත වන්නට වන අතර, ඔවුන්ගේ නම් අපි ලිපියේ අවසානයේ සඳහන් කරමු.
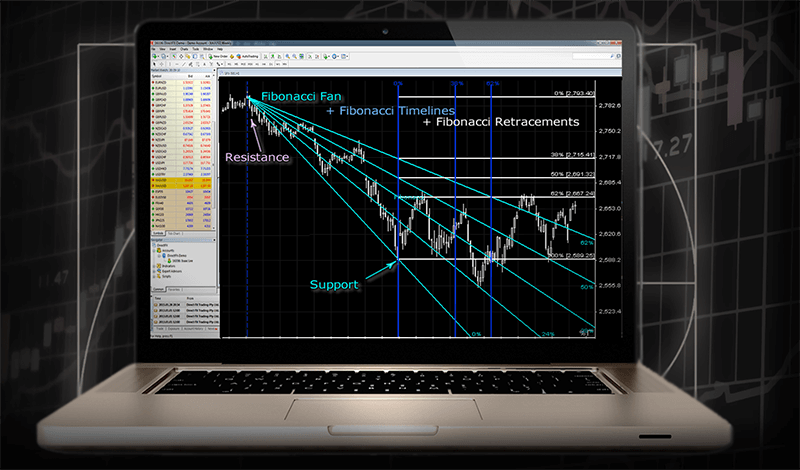
Fibonacci නැවත ලබා ගැනීමේ මට්ටම්
ඉතාලි ගණිතඥයාගේ නමින් නම් කරන ලද තාක්ෂණික විශ්ලේෂණයේ වඩාත්ම ජනප්රිය මෙවලම වන්නේ Fibonacci Retracement මට්ටම් වන අතර, ප්රධාන ප්රවණතාවයේ සිට මිල නිවැරදි කිරීමේ ප්රමාණය තීරණය කිරීම සඳහා භාවිතා කරනු ලැබේ. වඩාත් පොදු retracement මට්ටම් 23.6%, 38.2%, 50%, 61.8%, සහ සමහර විට 78.6% වේ. මෙම මට්ටම් යෙදීම සඳහා, පළමුව මිල සටහනේ ඇති ප්රධාන ප්රවණතාවය හඳුනාගත යුතුය. ඉන්පසුව, MT4 පර්යන්තයේ, Draw Fibonacci retracement මෙවලම මෙම ප්රවණතාවයේ ආන්තික ලක්ෂ්ය දෙකට යොදනු ලැබේ: ඉහළ ප්රවණතාවක් සඳහා අවම සහ උපරිම හෝ පහත වැටීමක් සඳහා උපරිම සහ අවම වේ. ප්රස්ථාරයේ ප්රතිඵලයක් ලෙස ලැබෙන Fibonacci මට්ටම් මිලට ආධාරක හෝ ප්රතිරෝධය අත්විඳිය හැකි කලාප හඳුනා ගැනීමට සහ ඒ අනුව ආපසු හැරවීමට උපකාරී වේ.
විචක්ෂණශීලී පාඨකයෙකු Fibonacci අංක සහ Fibonacci retracement මට්ටම් අතර වෙනස වහාම දකිනු ඇත. මුලින්ම බැලූ බැල්මට ඔවුන් සම්බන්ධයක් නැති බව පෙනේ, නමුත් මෙය එසේ නොවේ.
– 23.6% මට්ටම ගැඹුරු අනුපාතයක් ලෙස ව්යුත්පන්න වන්නේ සංඛ්යාවක් අනුපිළිවෙලෙහි දකුණට ස්ථාන දෙකකින් පිහිටා ඇති සංඛ්යාවෙන් බෙදූ විටය.
- 38.2% මට්ටම Fibonacci අනුපිළිවෙලෙහි අංකයක් එහි දකුණට වහාම පිහිටා ඇති අංකයෙන් බෙදීමෙන් ප්රතිඵලය වේ. උදාහරණයක් ලෙස, 34 න් 89 න් බෙදීම ආසන්න වශයෙන් 0.382 ක් ලැබේ.
– 61.8% මට්ටම (හෝ 38.2% ක ප්රතිලෝම) ලබා ගන්නේ Fibonacci අනුක්රමයේ සංඛ්යාවක් එය සෘජුවම අනුගමනය කරන සංඛ්යාවෙන් බෙදීමෙනි. උදාහරණයක් ලෙස, 55 89 න් බෙදීම ආසන්න වශයෙන් 0.618 වේ.
- 50% මට්ටම Fibonacci අනුක්රමය යෙදීමේ සෘජු ප්රතිඵලයක් නොවේ, නමුත් එය බොහෝ විට එහි සරල බව සහ මනෝවිද්යාත්මක වැදගත්කම හේතුවෙන් තාක්ෂණික විශ්ලේෂණයේ දී භාවිතා වේ. බොහෝ විට මිල ගණන් පෙර චලනයෙන් අඩකින් පමණ නිවැරදි වන බව නිරීක්ෂණය වී ඇත.
- 78.6% මට්ටම 61.8% හි වර්ගමූලයයි.
Fibonacci Extension මට්ටම්
විස්තාරණ මට්ටම් නිවැරදි කිරීමකින් පසු ප්රාථමික ප්රවණතාවයේ දිශාවට මිල චලනය දිගටම කරගෙන යා හැකි මට්ටම් තීරණය කිරීමට යොදා ගනී. 161.8%, 261.8%, සහ 423.6% ඇතුළුව මෙම මට්ටම්, වෙළඳපල චලනයන් බොහෝ විට ස්වභාවධර්මයේ සහ ගණිතයේ ඇති සමානුපාතිකයන් අනුගමනය කරයි යන උපකල්පනය මත පදනම් වේ. නිවැරදි කිරීමක් සම්පූර්ණ කිරීමෙන් පසු වෙළඳ ස්ථාන වසා දැමීම හෝ ලාභ ලබා ගැනීම සඳහා ඉලක්ක හඳුනා ගැනීමට දිගු කිරීම් වෙළඳුන්ට සහාය වේ. Fibonacci අනුක්රමයේ සංඛ්යා නොවුවද, මෙම මට්ටම් ගණිතමය ගුණාංග හරහා එයට සමීපව සම්බන්ධ වේ, විශේෂයෙන් රන් අනුපාතය (1.618).
- 161.8% සෘජුවම ප්රතිඵලය වන්නේ රන් අනුපාතිකය 100 න් ගුණ කිරීමෙනි. මෙම විස්තාරණ මට්ටම එය රන් අනුපාත සංගුණකයෙන් ගුණ කළ පෙර ප්රවණතාවයට සමානුපාතික විය හැකි ලක්ෂ්යයට අනුරූප වන බැවින් මෙම දිගු මට්ටම විශේෂයෙන් වැදගත් වේ. Fibonacci අනුපිළිවෙලෙහි සන්දර්භය තුළ, ඔබ කිසියම් අංකයක් ගෙන එය 1.618 කින් ගුණ කළහොත්, ඔබ අනුපිළිවෙලෙහි ඊළඟ අංකයේ අගය ආසන්න වශයෙන් ගණනය කරනු ඇත.
- 261.8% සහ 423.6% ද ස්වර්ණමය අනුපාතයට සම්බන්ධ ප්රතිශත වන නමුත් නිවැරදි කිරීමකින් පසුව දිගු හෝ වැඩි ආන්තික ඉලක්ක මට්ටම් නියෝජනය කරයි. උදාහරණයක් ලෙස, ස්වර්ණමය අනුපාතය (1.618) විසින්ම ගුණ කිරීමෙන් සහ එය ප්රතිශතයක් බවට පරිවර්තනය කිරීම සඳහා 100 න් ගුණ කිරීමෙන් 261.8% ව්යුත්පන්න කළ හැක. මෙම මට්ටම මිල සංචලනය සඳහා තවත් ඉලක්කයක් පෙන්නුම් කරයි, එය ශක්තිමත් ප්රවණතා වලදී විශේෂයෙන් අදාළ විය හැකිය. 423.6% ලබාගන්නේ ස්වර්ණමය අනුපාතය තවදුරටත් ගුණ කිරීමෙන් හෝ Fibonacci සංඛ්යා වෙනත් සංයෝජන මගින් තමන් විසින්ම සහ 100 කින් ගුණ කිරීමෙනි. මෙම මට්ටම ඊටත් වඩා ආන්තික ඉලක්කයක් නියෝජනය කරයි, එය ඉතා ප්රබල ප්රවණතා චලනයන්හි දුර්ලභ අවස්ථාවන්හිදී ළඟා විය හැකිය.
ප්රායෝගික යෙදුම් ඉඟි
Fibonacci retracement සහ extension level යනු පළපුරුදු වෙළෙන්දෙකු සඳහා ප්රබල මෙවලමක් වන අතර, වෙළඳපල හැසිරීම අනාවැකි පල කිරීමේ ඉහළ සම්භාවිතාවක් ලබා දෙයි. කෙසේ වෙතත්, ඕනෑම මෙවලමක් මෙන්, ඔවුන් 100% සහතිකයක් ලබා නොදෙන බව මතක තබා ගැනීම වැදගත්ය. එබැවින් දැඩි අවදානම් කළමනාකරණ විනය නිරීක්ෂණය කළ යුතු අතර, වඩාත් විශ්වාසදායක ලබා ගැනීම සඳහා Moving Averages (MA), Relative Strength Index (RSI), MACD සහ පරිමා මට්ටම් වැනි වෙනත් තාක්ෂණික විශ්ලේෂණ ක්රම සහ දර්ශක සමඟ වෙළඳාමට ඇතුල් වීම හෝ පිටවීම සඳහා සංඥා ඒකාබද්ධව ඒවා භාවිතා කළ යුතුය. විවිධ කාල රාමු සලකා බැලීම ද වැදගත්ය. නිදසුනක් ලෙස, දෛනික හෝ සතිපතා ප්රස්ථාරවල හඳුනාගෙන ඇති Fibonacci මට්ටම් කෙටි කාල රාමුවලට වඩා ප්රබල ආධාරක හෝ ප්රතිරෝධක මට්ටම් සපයන ඒවාට වඩා වැදගත් විය හැක.
Fibonacci මට්ටමක් මත පදනම්ව වෙළඳාමකට ඇතුල් වීමට තීරණය කිරීමට පෙර, කැන්ඩල්ස්ටික් රටා වැනි තහවුරු කරන සංඥා සඳහා රැඳී සිටීම සුදුසුය. අතිරේකව, Draw Fibonacci retracement මෙවලම යොදන විට, ආරම්භක සහ අවසන් ස්ථාන නිවැරදිව තෝරා ගැනීම ඉතා වැදගත් වේ. ප්රස්ථාරයේ පැහැදිලිව නිර්වචනය කර ඇති ඉහල හෝ පහල ස්ථාන තෝරාගත යුතුය.
Fibonacci මට්ටම් වලට ප්රයෝජනවත් මිණුම් සලකුණු සැපයිය හැකි අතර, ඒවා දැඩි නීතියකට වඩා මනෝවිද්යාත්මක සාධකයක් නියෝජනය කරන බැවින්, වෙළඳපල සෑම විටම අනාවැකි පල කළ හැකි ලෙස ඒවාට ප්රතිචාර නොදක්වන බව වටහා ගැනීම අත්යවශ්ය වේ. එබැවින්, වෙළඳුන් අනපේක්ෂිත චලනයන් සඳහා සූදානම් විය යුතු අතර ඒ අනුව අවදානම් කළමනාකරණය කළ යුතුය. Stop Loss සහ Take Profit orders සැකසීමෙන් මෙයට සහය විය හැකිය. උදාහරණයක් ලෙස, ව්යාජ බිඳවැටීම් වලින් ආරක්ෂා වීමට ප්රධාන Fibonacci මට්ටමෙන් ඔබ්බට Stop Loss එකක් තැබිය හැක.
තාක්ෂණික විශ්ලේෂණ මෙවලම්
Fibonacci මට්ටම් මත පදනම් වූ බොහෝ මෙවලම් තිබේ. Fibonacci Retracement යනු අපි දැනටමත් සාකච්ඡා කර ඇති වෙළඳුන් අතර වඩාත් ජනප්රියයි. එය MetaTrader 4 පර්යන්තයට ඒකාබද්ධ කර ඇති අතර, එය Draw Fibonacci Retracement ලෙස හැඳින්වේ. තවත් මෙවලමක් වන Fibonacci Extension ද සාකච්ඡා කර ඇත.
Fibonacci Projections යනු Fibonacci Extension හා සමාන මෙවලමකි. වෙනස වන්නේ එය පෙර ගමන් තරංගවල ප්රමාණය සහ දිශාව මත පදනම්ව පසුකාලීන මිල චලනය තක්සේරු කිරීමට ක්රමයක් ඉදිරිපත් කිරීමයි. අනාගත චලනය පිළිබඳව අනාවැකි පල කිරීම සඳහා, පෙර තරංගයේ ලක්ෂ්ය තුනක් තෝරාගත යුතුය: ව්යාපාරයේ ආරම්භය, ව්යාපාරයේ අවසානය සහ නිවැරදි කිරීමේ අවසන් ස්ථානය.
තවත් මෙවලමක් වන Fibonacci Fan, ප්රස්ථාරයේ ඇති Fibonacci retracement මට්ටම් හරහා එක් ලක්ෂ්යයකින් (සාමාන්යයෙන් සැලකිය යුතු අවම හෝ උපරිමයක්) අඳින ලද රේඛා වලින් සමන්විත වේ. Fibonacci Fan රේඛා සිදුවිය හැකි ආධාරක හෝ ප්රතිරෝධක රේඛා ලෙස කටයුතු කළ හැකිය.
අවසාන වශයෙන්, Fibonacci Time Zones, තාක්ෂණික විශ්ලේෂණය සඳහා තරමක් අසාමාන්ය මෙවලමක්, ගත වූ කාලය මත පදනම්ව සිදුවිය හැකි ආපසු හැරවීමේ අවස්ථා හඳුනා ගැනීමට භාවිතා කරයි. කලාප සමන්විත වන්නේ නිශ්චිත කාල අන්තරවල තබා ඇති සිරස් රේඛා මාලාවකින් වන අතර, එය Fibonacci අනුපිළිවෙලට අනුරූප වන අතර මෙම අවස්ථාවන්හි වැදගත් ප්රතිවර්තන ලක්ෂ්යයන් ඇතිවිය හැකි බව යෝජනා කරයි.
කලින් සඳහන් කළ පරිදි, මෙම මෙවලම්, වෙනත් ඕනෑම දෙයක් මෙන්, අනාගත මිල චලනයන් පිළිබඳ නිවැරදි අනාවැකියක් සහතික නොකරයි. ඔවුන් වෙළඳ මෙහෙයුම් සැලසුම් කිරීමේදී සහ වෙළඳ උපාය මාර්ග සංවර්ධනය කිරීමේදී සලකා බැලිය යුතු මට්ටම් පමණක් සපයයි. ලැයිස්තුගත මෙවලම් සාර්ථක ලෙස යෙදීම සඳහා පුහුණුවීම්, ඉවසීම, විනය සහ වෙළඳපල තත්ත්වයන් පිළිබඳ ගැඹුරු අවබෝධයක් අවශ්ය වේ..
තවදුරටත් ඉතිහාසය: 13 සිට 20 වැනි සියවස දක්වා
ප්රධාන ගණිත නිබන්ධනය වන "Liber Abaci" (ගණනය කිරීමේ පොත) ෆිබොනාච්චි විසින් 1202 දී ලියා ඇති අතර සංශෝධිත සංස්කරණයක් 1228 දී ප්රකාශයට පත් විය. මෙම පොත දශම ගණිතය ප්රදර්ශනය කිරීම සහ ප්රවර්ධනය කිරීම සඳහා කැප වූ අතර ශුන්ය සංඛ්යාව නියෝජනය කිරීම ඇතුළුව ඉන්දු-අරාබි ඉලක්කම් වලින් ව්යාප්තිය සඳහා අඩිතාලම දැමීය. මෙම කාර්යයේදී, හාවුන්ගේ ජනගහන වර්ධනය පිළිබඳ ගැටළුවක් විසඳන අතරතුර, ෆිබොනාච්චි ඔහුගේ නම දරන සුප්රසිද්ධ අනුපිළිවෙල සකස් කළ අතර එය ගණිතයට ඔහුගේ වඩාත්ම වැදගත් දායකත්වය බවට පත්ව ඇත.
Fibonacci අනුපිළිවෙල 20 වන සියවසේ මූල්ය වෙලඳපොලවල් වෙළඳාම් කිරීමේදී නව යෙදුමක් සොයා ගන්නා ලදී, මූලික වශයෙන් එය අධ්යයනය කර එය භාවිතා කළ වෙළඳුන් කිහිප දෙනෙකුට සහ මූල්ය විශ්ලේෂකයින්ට ස්තූතිවන්ත විය. ඒවායින් බොහොමයක් මිල රටා සහ එලියට් තරංග න්යාය සමඟ Fibonacci මට්ටම් සම්බන්ධ කර ඇත. රැල්ෆ් එලියට්ගේ කෘතිය පුනරාවර්තන රටා සහ අනුපිළිවෙල මත පදනම් වුවද, එය සාකච්ඡා කරන ලද අනුපිළිවෙල සමඟ සම්බන්ධයක් සොයා ගනී. වෙළඳපල තරංග රටා Fibonacci සංඛ්යා වලට තරමක් සම්බන්ධ ව්යුහයක් අනුගමනය කරන බව එලියට් සොයා ගත්තේය. නිදසුනක් වශයෙන්, තරංග 5 සහ 3 ඛණ්ඩවලට බෙදීම, 8 දක්වා එකතු කිරීම, Fibonacci අනුපිළිවෙලෙහි කොටසකි. එලියට්ගේ අනුගාමිකයෙකු වන රොබට් ප්රෙච්ටර්, වෙළඳපල තරංග සමූහ මනෝවිද්යාව අනුගමනය කරන බව ප්රකාශ කරමින්, සත්ය වශයෙන්ම මෙම රටා ෆිබොනාච්චි අංක භාවිතයෙන් අනාවැකි කළ හැකි බව පැහැදිලිව පෙන්නුම් කළේය.
Larry Pesavento තාක්ෂණික විශ්ලේෂණයේ දී Fibonacci මට්ටම් භාවිතය ප්රචලිත කිරීමට සැලකිය යුතු දායකත්වයක් ලබා දුන්නේය. මෙම වෙළඳ ප්රවීණයා සුසංයෝගී මිල රටා ගවේෂණය කරමින් පොත් රාශියක් ලිවීය, ඒවායින් බොහොමයක් ඉතාලි ගණිතඥයාගේ අනුපිළිවෙලට සමීපව සම්බන්ධ වී ඇත. Scott Carney විසින් Fibonacci මට්ටම් මත පදනම්ව "Butterfly" සහ "Crab" වැනි සුසංයෝග රටා කිහිපයක් ද නිර්මාණය කරන ලදී. Philip Carret ගේ දායකත්වය ද අමතක නොකළ යුතුය. පුරෝගාමී අරමුදලේ නිර්මාතෘ වෙලඳපොල විශ්ලේෂණය කිරීම සඳහා ගණිතමය මූලධර්ම භාවිතා කළ අතර, දිගුකාලීන විශ්ලේෂණය සහ කොටස් තෝරාගැනීම මත පදනම්ව ආයෝජනය සඳහා ඔහුගේ ප්රවේශය, "රන් අනුපාතය" සෙවීමට සමාන මූලධර්ම පිළිබිඹු කරයි.
***
අවසාන වශයෙන්, මූල්ය විශ්ලේෂණයේ දී Fibonacci මට්ටම්වල වැදගත්කම සහ ප්රයෝජනය පිළිබඳ බොහෝ වෙළඳුන්ගේ සහ විශ්ලේෂකයින්ගේ පොදු මතය පිළිබිඹු කරන ප්රකාශ කිහිපයක් ඉදිරිපත් කරමු:
- "Fibonacci අනුපිළිවෙල යනු විශ්වයේ ස්වාභාවික අනුපිළිවෙලයි, එබැවින් අනාගත චලනයන් පිළිබඳව අනාවැකි පල කිරීම සඳහා මූල්ය වෙලඳපොලවල් වෙත එය යෙදීම පරිපූර්ණ වශයෙන් අර්ථවත් කරයි."
- "Fibonacci retracement මට්ටම් වෙළඳාමේ ශුද්ධ වූ බඳුනක් නොවේ, නමුත් ඒවා වෙළඳපල මනෝවිද්යාව සහ සිදුවිය හැකි ආපසු හැරවීම් අවබෝධ කර ගැනීම සඳහා ඇදහිය නොහැකි තරම් ප්රයෝජනවත් වේ."
- "Fibonacci දිගු කිරීම් ප්රවණතා වෙළඳපලක ලාභ ඉලක්ක තැබීම සඳහා අගනා වේ, මිල මීළඟට යා හැකි ස්ථානයට මාර්ග සිතියමක් ඉදිරිපත් කරයි."
ආපසු යන්න ආපසු යන්න
